Eis am Stiel
Shutterstock/photka
Eis am Stiel für Kombinierer
Mit unserem kostenlosen Lernmaterial können Schüler:innen unterschiedliche Kombinationen aus Tüten, Eiskugeln und Toppings zusammenstellen.
So lassen sich im Mathematik-Unterricht einfache kombinatorische Abzählaufgaben anschaulich durchführen.
Kompetenzbereich „Daten und Zufall“ - Lösen von Abzählaufgaben
Der neue Lehrplan sieht im Kompetenzbereich „Daten und Zufall“ das Lösen einfacher Abzählaufgaben bereits in der 5. Schulstufe vor.
VERITAS-Mathematikbuch Zahlen, bitte! 1
Im VERITAS-Mathematikbuch Zahlen, bitte! 1 findet sich dafür ein spezielles Lernspiel, das die Schüler:innen selbst ausdrucken und zusammenfalten können. Das Material „Kombinatorischer Eisgenuss“ steht als kostenloser Download auch auf scook.
Wie funktioniert‘s?
Auf der Spielseite, die jedem Exemplar von Zahlen, bitte! 1 beiliegt, befinden sich drei Körpernetze (zwei Würfel und ein dreiseitiges Prisma).
Die Schüler:innen schneiden die Körpernetze und die schraffierten Kreisflächen aus und malen die Abbildungen auf den Körpernetzen mit unterschiedlichen Farben an.
Anschließend kleben sie die Körper an den grauen Klebeflächen zusammen. Die Körper können nun auf einen Stift (z.B. Bleistift) gesteckt werden: unten der Würfel mit den Eistüten, in der Mitte der Würfel mit den Eiskugeln, oben das dreiseitige Prisma mit den Toppings.
Nun können die Schüler:innen durch Drehen der drei Körper unterschiedliche Tüten-Eis-Topping-Kombinationen erstellen und dabei selbst herausfinden, wie viele Kombinationen möglich sind. Dafür sollen sie die einzelnen Kombinationen schriftlich festhalten oder fotografieren, in weiterer Folge können sie das Multiplikationsprinzip selbst entdecken.
Durch Abzählen oder Anwenden der Multiplikationsregel erkennen die Schüler:innen schließlich, dass es bei 4 Eistüten, 4 Eiskugeln und 3 Toppings genau 4 x 4 x 3 = 48 mögliche Kombinationen gibt.
Differenzierung: So wird’s leichter!
Für einen einfacheren Zugang kann die Aufgabe zunächst auch mit nur zwei Würfeln durchgeführt werden: Tüten und Eiskugeln.
Dadurch ergeben sich weniger Kombinationen, nämlich
4 x 4 = 16.
Gerade leistungsschwächere Schüler:innen tun sich mit dieser reduzierten Variante leichter. Auf diese Art eignet sich das Drehspiel auch für die Volksschule, wo einfache kombinatorische Abzählaufgaben in der 3. Klasse am Lehrplan stehen.
Baumdiagramme
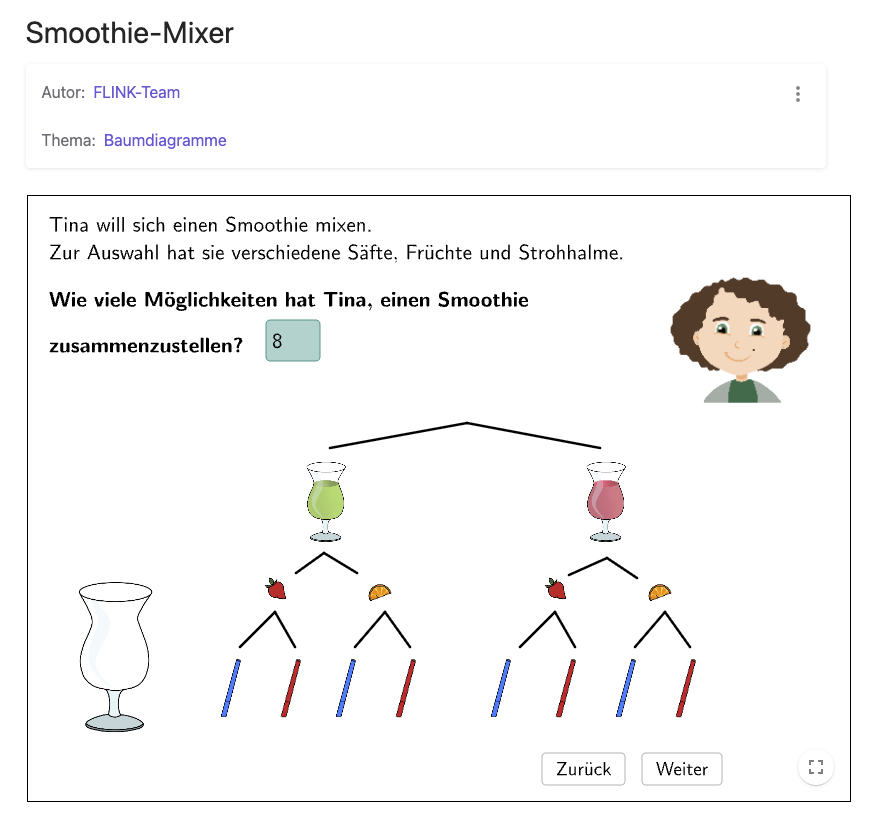
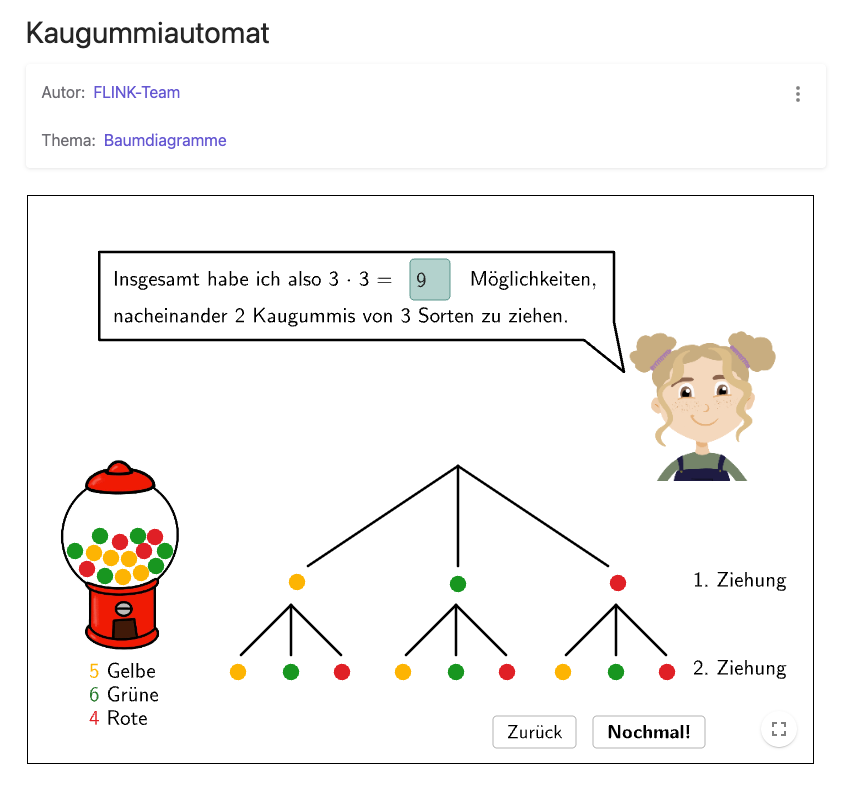
Nach dem haptischen, dreidimensionalen Einstieg ins Thema folgt der Übergang auf die zweidimensionale Ebene, zum Beispiel mit dem Baumdiagramm. Im Schulbuch Zahlen, bitte! 1 findet man dafür einige spezielle Aufgaben (753, 754, 755), außerdem gibt es dazu ein kostenloses Erklärvideo auf scook.
Für die digitale Erarbeitung von Baumdiagrammen im 5. Schuljahr stellt die Initiative FLINK in Mathe der Johannes Kepler Universität Linz kostenlose Abzählaufgaben mit Baumdiagrammen zur Verfügung. Dabei können die Schüler:innen eigenständig entdecken, wie Abzählaufgaben mit Baumdiagrammen dargestellt werden und wie die Multiplikationsregel bei Abzählaufgaben anzuwenden ist.
Tipp
Tipp: Als Bonusaufgabe eignet sich der FLINK-Kind-Generator auf der FLINK-Webseite.
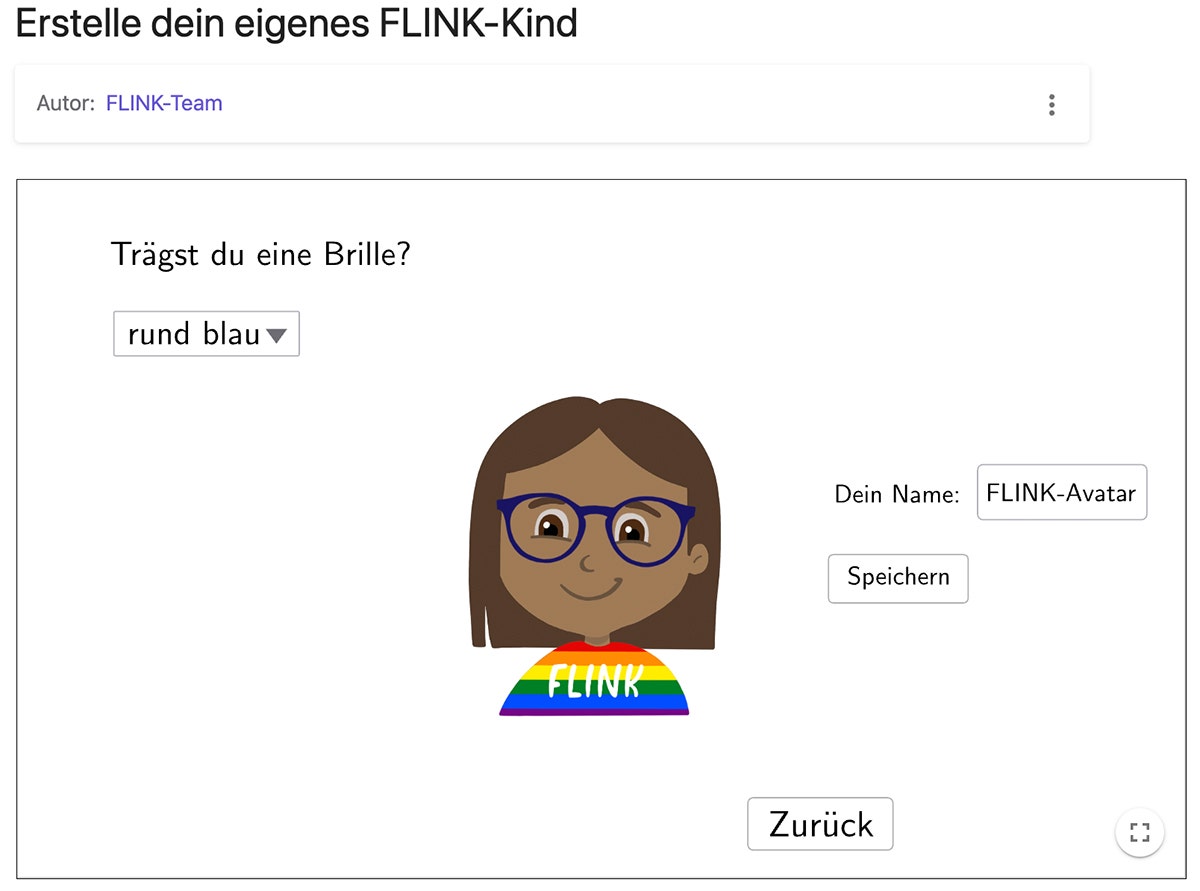
Damit können Schüler:innen selbst eigene „FLINK-Kinder“ erstellen und beliebig gestalten (Haut-, Augen- und Haarfarbe, Frisur, Kleidung, Brille). Besonders leistungsstarke Schüler:innen sollen herausfinden, wie viele unterschiedliche FLINK-Kinder durch diesen Generator erzeugt werden können.
Hier die Antwort: Mit einer Auswahl von 4 Hautfarben, 4 Augenfarben, 9 Frisuren, 6 Haarfarben, 8 Kleidungsfarben und 6 Brillen ergeben sich gesamt 4 x 4 x 9 x 6 x 8 x 6 = 41.472 mögliche Kombinationen für ein eigenes FLINK-Kind.
Carina Schobersberger, BA, BEd, MEd ist Mathematiklehrerin an der Mittelschule Alkoven. Sie entwickelt an der Johannes Kepler Universität Linz digitale Lehr- und Lernmaterialien für FLINK in Mathe und erstellt Zusatzmaterialien für die Schulbuchreihe „Zahlen, bitte!“. ...
